Método Matricial de las Rigideces en vigas

 

¿Qué es una viga ?

Una viga es una estructura recta , que es apoyada y cargada de tal manera que todas sus fuerzas externas y momentos que actúan sobre ella se encuentran en un plano de simetría de su sección transversal,con todas las fuerzas perpendiculares a su eje centroidal.

Bajo la acción de cargas externas, las vigas están sujetas solo a Momentos de flexión y Fuerzas de corte (sin fuerzas axiales).Pueden poseer hasta dos grados de libertad por nudo.

Imagen 1 : Ejemplo de una viga con dos apoyos simples y un apoyo fijo.

  - Método de rigideces:

El método de rigideces obedece a la siguiente ecuación matricial:

[F] = [K][U]

Donde:

[F] : Matriz de fuerzas

[K] : Matriz de rigidez

[U] : Matriz de desplazamientos

- Matriz de rigidez [K]:

Para el análisis por el metodo de rigideces en vigas, se dividirá la estructura en tramos, y se obtendrá la matriz de rigidez de cada elemento , para después ensamblar las matrices obtenidas en una sola matriz , llamada Matriz de rigidez global.

Imagen 2 : Matriz de rigidez para una viga sin considerar efectos por corte.

Donde:

E : Módulo de elasticidad.

I : Inercia con respecto al eje "Z".

L : Longitud del tramo.

u₁,u₃ : Dformaciones en el eje "Y".

u₂,u₄ : Giros con respecto al eje "Z".

La matriz antes mencionada solo considera los efectos por flexión,ya que en la mayoria de los casos los efectos por corte suelen ser despreciables. 

- Procedimiento:

1. Se dividirá la viga en tramos , para despues determinar los grados de libertad de la estructura.

Imagen 3 : Grados de libertad de la viga mostrada en la imagen 1.

El grado de la Matriz de rigidez global dependerá de los grados de libertad que posea la estructura , en este caso la viga posee 5 grados de libertad por lo cual la Matriz de rigidez global será de 5x5.

2. Se obtendrá la matriz de rigidez de cada tramo.

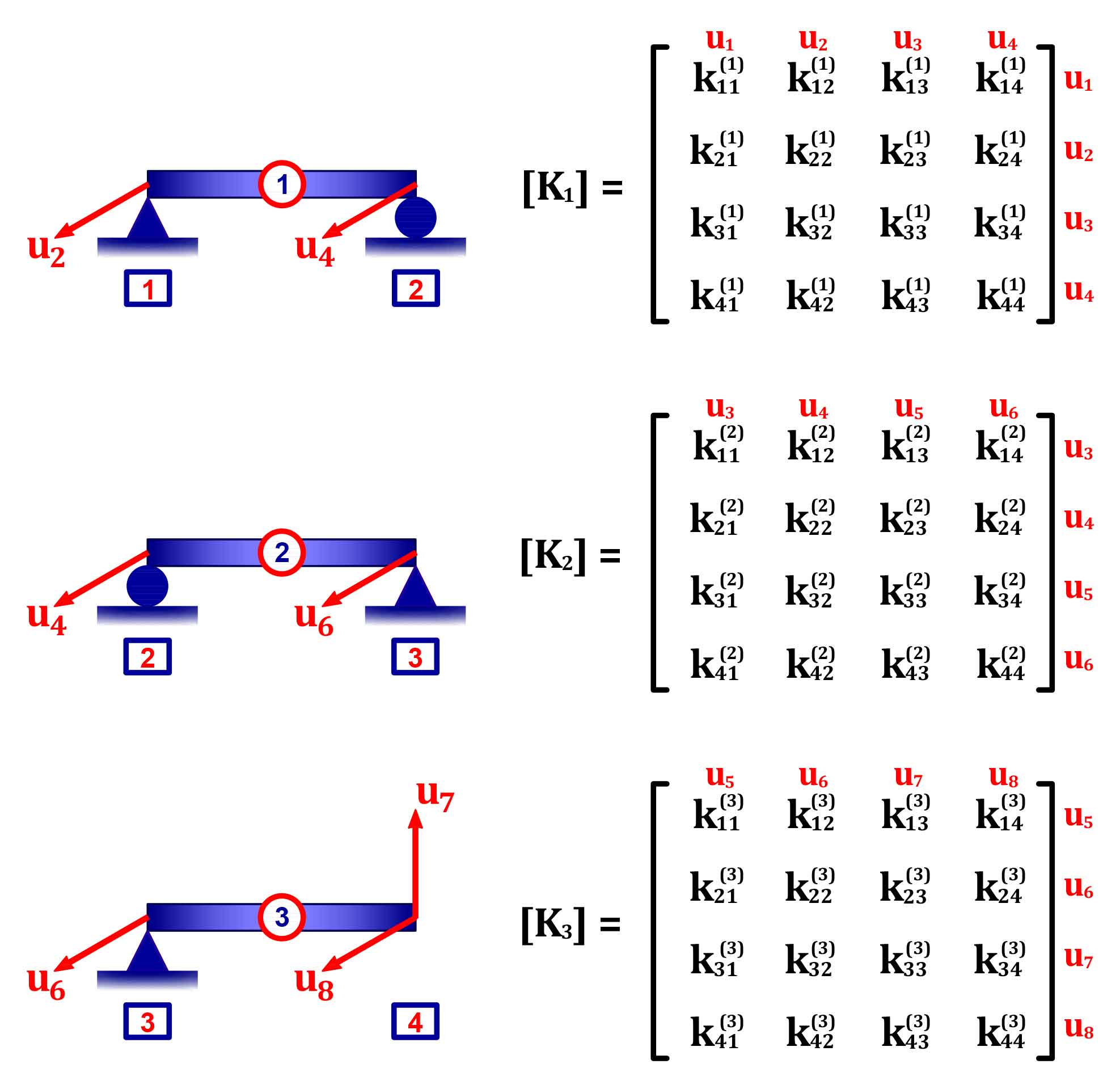Imagen 4 : Matriz de rigidez por tramos para la viga mostrada en la imagen 1.

3. Ensamblaje de la Matriz de rigidez global.

 

Imagen 5 : Ensamblaje de Matriz de Rigidez Global.

Las filas y columnas u1, u3, u5 se eliminaran de las matrices de rigidez,ya que no existe desplazamientos verticales en los apoyos 1,2 y 3.

4. Se calculará los Momentos de Empotramiento Perfecto y Fuerzas de fijacion,de cada tramo para poder obtener la Matriz de vectores de fijacion [F⁰].

Imagen 6 : Matriz de Vectores de fijación y momentos de empotramiento perfecto de la viga motrada en la imagen 1.

5. Ensamblaje de Matriz de Vectores de Fijación Global [F⁰].

Imagen 7 : Ensamblaje de Matriz de vectores de fijacion global de la viga mostrada en la imagen 1.

6. Obtención de la Matriz de fuerzas externas [Fᵉ].

 

Imagen 8 : Matriz de fuerzas externas de la viga mostrada en la imagen 1. 

Las matriz de fuerzas externas vienen a estar conformadas por fuerzas y momentos aplicados en los extremos de cada tramo de la viga, en este caso no existen fuerzas externas ,por lo tanto la matriz de fuerzas externas será nula.  

7. Aplicación de la expresión matricial del método de rigideces.

Imagen 9: Obtencion de la matriz de desplazamientos global de la viga mostrada en la imagen 1.

 8. Obtención de matrices de desplazamiento por tramos.

Imagen 10 : Matriz de desplazamiento de la viga mostrada en la imagen 1.

9. Proceso de retorno y cálculo de reacciones para cada tramo de la viga.

Imagen 11 : Proceso de retorno y cálculo de reacciones de la viga mostrada en la imagen 1.